This numerical model was developed for the project “Adaptive numerical modeling of atmospheric moist convection“. It uses the function library amatos (by Jörn Behrens) for managing the adaptively refined triangular grid. The discontinuous Galerkin method developed in cooperation with Francis X. Giraldo.

Movies of test cases:

without artificial viscosity: (no flux limiter causes noisy results)

• 1000m x 1000m domain:
  

  smooth warm air bubble (Giraldo and Restelli, 2008)

  HQ (37MB)

  MQ (13MB)

  LQ (3MB)

with artificial viscosity µ=0.1m²/s:

• 1000m x 1000m domain:
  

  smooth warm air bubble (Giraldo and Restelli, 2008)	HQ (35MB)	MQ (11MB)	LQ (2MB)
  small cold air bubble on top of large warm air bubble (Robert, 1993)	HQ (27MB)	MQ (8MB)	LQ (2MB)

• 1000m x 1500m domain:
  

  smooth warm air bubble (Robert, 1993)

  HQ (63MB)

  MQ (19MB)

  LQ (5MB)

• with diffusion µ=75m²/s:
  

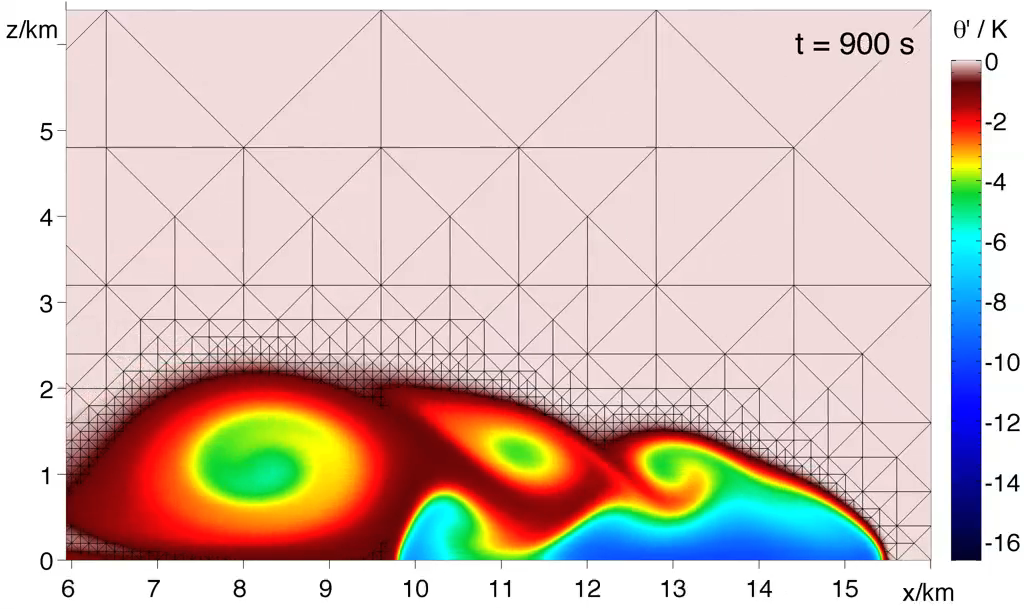
  density current (Straka et. al, 1993)

  HQ (33MB)

  MQ (10MB)

  LQ (3MB)

Movies of sensitivity studies:

Some details of the numerical model:

• compressible Euler equations with artificial viscosity
• solid-wall boundaries
• conforming triangular grid: h-adaptive refinement managed by the function library amatos (by J. Behrens) with space filling curve approach
• discontinuous Galerkin code (in cooperation with F.X. Giraldo)
• order of polynomials: up to 15th order implemented
• based on strong-formulation and a nodal DG method
• numerical flux: Rusanov-flux
• time-integration: explicit Runge-Kutta or IMEX-method with BDF2
• conserving mass (on grid coarsening by adjusting the constant of the polynomials)
• refinement criterion: θ’≥ σ max(θ’) (θ‘: deviation of the potential temperature from background state, threshold σ: usually σ = 0.1) plus 2 or 3 fine elements surrounding the refinement area.